(PUC-SP) Em uma máquina de Atwood ideal, são presas duas massas, tais que M1>M2
07. (PUC-SP) Em uma máquina de Atwood ideal, são presas duas massas, tais que M1>M2. Inicialmente as massas estão em repouso e niveladas. Após o abandono simultâneo das massas, verifica-se que a energia total do sistema é de 100J, após elas terem percorrido 5m em 2s, alcançando uma velocidade de 5,0m/s. Sabendo que o módulo da aceleração da 2 gravidade é de 10m/s2 , determine, em kg, os valores de cada uma das massas.
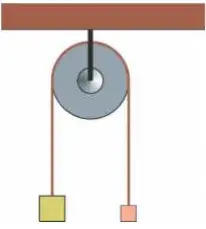
- M1=6,0 e M2=2,0
- M1=6,5 e M2=1,5
- M1=4,5 e M2=3,5
- M1=5,0 e M2=3,0
Resposta: D
Resolução:
Para resolver esse problema, podemos aplicar as equações de movimento na máquina de Atwood. Vamos considerar as seguintes informações:
Massas: M1 e M2
Energia total do sistema: 100 J
Deslocamento: 5 m
Tempo: 2 s
Velocidade final: 5,0 m/s
Aceleração da gravidade: 10 m/s²
A energia total do sistema é composta pela energia cinética das massas M1 e M2. Portanto, podemos escrever a seguinte equação:
Energia total = Energia cinética de M1 + Energia cinética de M2
1/2 * M1 * V1² + 1/2 * M2 * V2² = 100
Sabemos que a velocidade final de ambas as massas é igual a 5,0 m/s. Portanto, podemos escrever:
1/2 * M1 * (5,0 m/s)² + 1/2 * M2 * (5,0 m/s)² = 100
25/2 * M1 + 25/2 * M2 = 100
Simplificando a equação, temos:
25 * (M1 + M2) = 200
M1 + M2 = 8
Agora, vamos analisar a relação entre as massas e as acelerações. Na máquina de Atwood, a aceleração é dada pela diferença das massas multiplicada pela aceleração da gravidade. Portanto, temos:
a = (M1 - M2) * g
Substituindo o valor da aceleração da gravidade (g = 10 m/s²), temos:
a = 10 * (M1 - M2)
No intervalo de tempo de 2 s, a velocidade varia de 0 m/s para 5,0 m/s. Portanto, podemos escrever a equação da velocidade em função da aceleração e do tempo:
V = a * t
5,0 m/s = a * 2 s
a = 2,5 m/s²
Agora, substituindo o valor da aceleração na equação da aceleração, temos:
2,5 m/s² = 10 * (M1 - M2)
Dividindo ambos os lados por 10, temos:
0,25 m/s² = M1 - M2
Agora, temos um sistema de equações:
M1 + M2 = 8
0,25 m/s² = M1 - M2
Podemos resolver esse sistema por substituição. Isolando M1 na segunda equação, temos:
M1 = 0,25 m/s² + M2
Substituindo esse valor na primeira equação, temos:
0,25 m/s² + M2 + M2 = 8
2,25 M2 = 7,75
M2 ≈ 3,44 kg
Substituindo esse valor na primeira equação, temos:
M1 + 3,44 kg ≈ 8
M1 ≈ 4,56 kg
Portanto, os valores aproximados para as massas são M1 ≈ 4,56 kg e M2 ≈ 3,44 kg.
A resposta correta é a letra D: M1 = 5,0 kg e M2 = 3,0 kg.